The current vogue for 'post-truth', (and post truth commentary about post-truth) is really a symptom of the post-modernist malaise which has afflicted universities for many decades. If it has become mainstream, it is not because of Trump or Brexit, but because of some very confused thinking about data analysis and information (I hinted at this here: http://dailyimprovisation.blogspot.co.uk/2012/09/appetite-will-and-intellect-journey-of.html). Now we have people like Nick Land spouting the language of second-order cybernetics and using it as an intellectual foundation for the alt-right. David Kernohan is partly right to say "This is us!" (here http://followersoftheapocalyp.se/its-good-to-be-king/) - but this isn't some kind of 'restoration'; it is simply madness, bad theory and weak thinking. This was always the danger with second-order cybernetics! So it's time to do some deeper (first-order?) cybernetic thinking and get back to the maths and to the detail of cybernetics - first and second-order. The place to start is at the root of the data fallacies and the assumptions about probability and counting.
When we count anything, a distinction is made between an inside and an outside. To count 2 of something is to perceive an analogy between thing 1 and thing 2. Ashby notes that:
When we count anything, a distinction is made between an inside and an outside. To count 2 of something is to perceive an analogy between thing 1 and thing 2. Ashby notes that:
"The principle of analogy is founded upon the assumption that a degree of likeness between two objects in respect of their known qualities is some reason for expecting a degree of likeness between them in respect of their unknown qualities also, and that the probability with which unascertained similarities are to be expected depends upon the amount of likeness already known."In other words, to say that a = b is to say that:
Here, the bracket around "Outside a" and "Outside b" (which encompasses a and b) represents a limit of apprehension of the outside of a and b. This limit, and the equating of the outsides of a and b are hypotheses. Even when we might think the similarity between things is obvious (as say between eggs), it remains a hypothesis. Which means that counting is a measure of the assumptions we make about perception, rather than any kind of indication of reality.
Information theory, which sees information as a measure of uncertainty about a message, and upon which much of our contemporary data analysis sits, is fundamentally about counting. This is what is represented in Shannon's formula:
Shannon does have an 'outside' for his measure on uncertainty (H) which he calls Redundancy (R). So we might write:
But there are a number of problems. Firstly, the Shannon formula represents a count of similar and dissimilar events; it is in effect a measure of the average surprisingness within a message. Each identification of similarity or dissimilarity is hypothetical (in the way described above), or unstable. Secondly, the denominator in the redundancy equation, Hmax, is a hypothesised number of the maximum possibilities for variation (as opposed to the observed variation).
For a system with N possible states, the number of total possible information (Hmax) is log(N). In identifying "a system" we have already made a distinction between the inside and the outside, and that in counting the number of possible states, we have already made a hypothesis about the context of similar states being the same. This is what we do when we describe something.
How many possible descriptions are there? Let's say there are M possible descriptions, which means that the total maximum entropy of the system + its descriptions is log(N x M). We may then produce descriptions about descriptions, which makes it log (N x M x O)... and so on.
But of course N, M or O cannot be known fully: there are an infinite range of descriptions and possibilities - we can only count the ones we know about. However, it is also true that descriptions N, M and O constrain each other. A description of the number of possible states is dependent on the number of possible states, and so on. These interactions of constraint may be analysed.
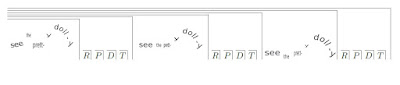
This can be illustrated with the example introduced by Jerome Bruner, of the mother playing with a child, presenting a dolly to her and saying "see the pretty dolly" (in "Child's Talk", 1983). The game is never played only once. It is repeated:
Each repetition is framed by previous repetitions. The mother (and probably the child) recognise that this is a repetition - except that it isn't exactly. In the diagram above, the differences in intonation, emphasis, timbre, etc are illustrated by the relative size and height of the words. Coming back to Ashby's comment about analogy, what assumptions are made if we say "the mother repeats the phrase three times"?
We can analyse each episode and describe each aspect. Calling the rhythm R, the pitch P, the timbre T, the dynamics D (and there are many other descriptions), then we might say that behind each of the utterances is a context RPTD.
Now the question is that in order to determine the similarity between these different utterances, an assumption is made about the similarity of the context. But for each description of each aspect of the context, there is also an assumption of similarity which is an assumption about its context. As so we get a recursive pattern:
(This misses out the final T). And on it goes. So each description constrains each other description. Might it then be possible to determine how each description might affect each other description?
One way this might be done is to consider the way that changes to one kind of description (say the rhythm) might be reflected in changes to another (say the pitch). To do this, it is not necessary to measure the redundancy. One only needs to measure the information as an index of the effects of the redundancy that sits behind it. If there are correlations between increases in information content (uncertainty) then there are is an indication of the mutual constraint between descriptions.
The next thing to consider is how it is that similarity is determined between these different variables. This can also tell us how new descriptions, and indeed surprises, might emerge.
The similarity between things - and their countability - is determined by the observer. Shannon information is not objective, and this, following Ashby, is an assumption about the unknown variables (the constraints) bearing upon the perception of something. The recursive pattern of distinctions and descriptions presented above is unstable because there is variation among the different recursions of the variables. Similarity is continually having to be asserted - a selection is made as to whether the latest utterance is the same or not. It may be that all one can say is "it might be" - and this is the essence of the game played between the mother and child.
So what when something surprising happens? What when half-way through playing this game, the mother says "BOO!". The child's question (and ours) concerns the assumptions they made about the context of the utterances "see the pretty dolly", and the fact that whatever context this was has now permitted a completely different kind of utterance. The surprise means that the assumptions about the context are wrong and need to change. "BOO!" cannot be admitted into the information system until a new understanding of the constraints of communication can admit "see the pretty dolly" and "BOO!" together.
Finally, what does this mean for truth? At one level, what we see as true fits the contextual knowledge we already possess. If the contextual knowledge is formed by the "echo chamber" of social media, it is quite easy to see how one might believe things to be true which others (with a better perspective) see as false. What we have become resistant to is to change and query our understanding of the context from which utterances emerge. Deep down this is an autistic trait: our society has become unempathic. The mother and child example, on the other hand, is the epitome of empathy.

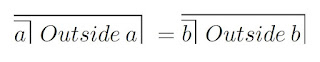




No comments:
Post a Comment