Cybernetics is full of 'spins'. From Watt governors to Heinz von Foerster's Eigenvalues, circular metaphors abound. This makes more sense when we can directly see the machine that makes it. But when the spin metaphor is applied to thinking itself, as with the Eigenforms, then I find that the description of the identification of objects as the emergence of stable patterns of flux in a continually emergent engagement between individuals and their environment difficult, if not downright fanciful. The assertion of those who believe this is that objects aren't 'real', what is seen as an object is a patterning of perception, notwithstanding philosophical arguments about 'real' in the first place.
Gordon Pask puts a similar emphasis on spins when he talks about concepts. He argues that
What do I think of this? It's difficulty is indicative of a bigger problem: it's simply all too circular. Spins are fascinating, but in the end, they just go round and round. I suspect everyone (including Von Foerster) got carried away with topology in the 60s and 70s and got caught up in its spins (everyone was into knots then: R.D. Laing and Lacan are (k)notable exponents!). It fitted the 'cybernetics of cybernetics' idea (although I'm fairly sure they misunderstood Margaret Mead's appeal - she had an eye on the circularity of cybernetic discourse, which Von Foerster's 'cybernetics of cybernetics' may have only made worse). It was as if they'd used mathematical topology for calculation of some hermetic wisdom: the maths became a positive metaphor for articulating what was the case with "thinking" and "perception". Yet topology, like all maths, is interesting where its reasoning breaks down: it articulates the limits of reasoning, albeit very complex reasoning.
For all this spinning, to me experience does not spin - it stretches in a process of tension and release. Music doesn't spin - the most spin-like music (for example, hypnotic trance music or minimalism) seems to me musically deficient. Curiosity is like this too, and for all these spinning accounts of cognition, curiosity precedes cognition. (Pask has an idea about the dynamics of concepts which appears to try to explain cognition, but it's all still spinning around).
There is at least some tension between Luhmann's psychic system and his social system. But the tension here (and indeed, the most sensible aspect of Luhmann's theory) is the fact that really he doesn't attempt to theorise what a psychic system is, only to say that it's what you and I do in our heads. For Luhmann, it's the communications we make which matter, which is a position with quite a Marxist practicality to it. He sensibly side-steps the issue of 'stretch'. The separation between psychic and social systems is what Luhmann gets criticised for by 2nd order cyberneticians. To me, it's a smart move, allowing him to say something practical without getting sucked-in to intractable arguments about thinking.
But characterising a stretch is difficult. Our physical analogues are usually biological in origin: the sinewy stretch of muscles, strings, elastic, and so on. But they could equally be psychological: stretching one's imagination, stretching a dissonance, prolonging moments.
The key difference between spins and stretches is a difference between sequentialism and recursion. That sounds like a strange statement, but I think I can explain it like this. A spin is conceived as a process of motion in time. The equation for a spin, as any circular motion is:
But what, really, is T? Ironically, the T is something which derives from clocks, which in turn depend on the same equation in order to operate, and the principal notion with regard to clocks is sequentialism (one thing follows another).
With a stretch something latent within a thing is revealed: the increased length of the elastic was always in the elastic. Whether the elastic is stretched or not, it is still elastic. The stretched elastic is always within the unstretched elastic as a potential. This is like saying that the infinite division of a line is always within the line (for example, the division in the Sierpinski triangle): the form that emerges is ever-present but unrealised. With the Sierpinski triangle, particularly, this indicates recursion as the operating principle.
But realisation of potential creates tension in elastic. But is the tension is really in us, not the elastic? It is our fingers that feel the force. And in our thinking about the division of the Sierpinksi triangle, as the recursion gets deeper so does the complexity, so does the tension we feel in apprehending what we witness.
But release is then interesting. We can of course release the elastic, which will take us back to where we started. But equally, we could do something with it which creates a new kind of stability. We can create some sort of tensegrity, which itself will have new latent recrusive properties. This, I think, is what concepts do. It may be that Pask is saying something similar. But I do suspect he gets it the wrong way round. Spins may be the product of stretches, not stretches the product of spins.
Gordon Pask puts a similar emphasis on spins when he talks about concepts. He argues that
Concepts are force exerting, persisting, closed, Brunnian in threes at least, braids recursively packed in toroidal processes ("like multicore telephone cable" or ""onion skins") in any medium, solid, liquid, gas, plasma or, indeed, brains. Their spins exert a residual parity within a coherence.What on earth does that mean? I suspect Pask saw concepts much as Von Foerster saw objects: a dynamic whose patterning forms (the "residual parity within a coherence") the basis of cognition. But it's a jolly abstruse concept!
What do I think of this? It's difficulty is indicative of a bigger problem: it's simply all too circular. Spins are fascinating, but in the end, they just go round and round. I suspect everyone (including Von Foerster) got carried away with topology in the 60s and 70s and got caught up in its spins (everyone was into knots then: R.D. Laing and Lacan are (k)notable exponents!). It fitted the 'cybernetics of cybernetics' idea (although I'm fairly sure they misunderstood Margaret Mead's appeal - she had an eye on the circularity of cybernetic discourse, which Von Foerster's 'cybernetics of cybernetics' may have only made worse). It was as if they'd used mathematical topology for calculation of some hermetic wisdom: the maths became a positive metaphor for articulating what was the case with "thinking" and "perception". Yet topology, like all maths, is interesting where its reasoning breaks down: it articulates the limits of reasoning, albeit very complex reasoning.
For all this spinning, to me experience does not spin - it stretches in a process of tension and release. Music doesn't spin - the most spin-like music (for example, hypnotic trance music or minimalism) seems to me musically deficient. Curiosity is like this too, and for all these spinning accounts of cognition, curiosity precedes cognition. (Pask has an idea about the dynamics of concepts which appears to try to explain cognition, but it's all still spinning around).
There is at least some tension between Luhmann's psychic system and his social system. But the tension here (and indeed, the most sensible aspect of Luhmann's theory) is the fact that really he doesn't attempt to theorise what a psychic system is, only to say that it's what you and I do in our heads. For Luhmann, it's the communications we make which matter, which is a position with quite a Marxist practicality to it. He sensibly side-steps the issue of 'stretch'. The separation between psychic and social systems is what Luhmann gets criticised for by 2nd order cyberneticians. To me, it's a smart move, allowing him to say something practical without getting sucked-in to intractable arguments about thinking.
But characterising a stretch is difficult. Our physical analogues are usually biological in origin: the sinewy stretch of muscles, strings, elastic, and so on. But they could equally be psychological: stretching one's imagination, stretching a dissonance, prolonging moments.
The key difference between spins and stretches is a difference between sequentialism and recursion. That sounds like a strange statement, but I think I can explain it like this. A spin is conceived as a process of motion in time. The equation for a spin, as any circular motion is:
With a stretch something latent within a thing is revealed: the increased length of the elastic was always in the elastic. Whether the elastic is stretched or not, it is still elastic. The stretched elastic is always within the unstretched elastic as a potential. This is like saying that the infinite division of a line is always within the line (for example, the division in the Sierpinski triangle): the form that emerges is ever-present but unrealised. With the Sierpinski triangle, particularly, this indicates recursion as the operating principle.
But realisation of potential creates tension in elastic. But is the tension is really in us, not the elastic? It is our fingers that feel the force. And in our thinking about the division of the Sierpinksi triangle, as the recursion gets deeper so does the complexity, so does the tension we feel in apprehending what we witness.
But release is then interesting. We can of course release the elastic, which will take us back to where we started. But equally, we could do something with it which creates a new kind of stability. We can create some sort of tensegrity, which itself will have new latent recrusive properties. This, I think, is what concepts do. It may be that Pask is saying something similar. But I do suspect he gets it the wrong way round. Spins may be the product of stretches, not stretches the product of spins.
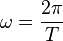
No comments:
Post a Comment